Salinan Soal Final OGM 7 Guru SMA ~ 17 April 2022

Selamat siang semua, berikut saya share salinan soal Final Olimpiade Guru Matematika (OGM) ke 7 bidang Guru SMA, yang dilaksanakan pada 17 April 2022.

Semoga bermanfaat.

1.      Berapakah bilangan bulat terkecil yang lebih besar dari $\sqrt{17+\sqrt3}+\sqrt{2022}$?

2.      Misalkan a, b, dan c merupakan barisan aritmatika dan a, b, a + c merupakan barisan geometri. Jika a, b, c merupakan bilangan bulat, maka berapakah nilai terkecil dari a + b + c ?

3.      Pak Andri dan Pak Dedy bersama 6 orang lainnya duduk dalam satu barisan. Jika peluang mereka tidak duduk bersebelahan adalah $p=\frac{a}{b}$, dimana $fpb(a,b)=1$, maka nilai a + b = ...

4.      Nala anak yang tekun belajar dan berkeinginan kuat untuk masuk jurusan kedokteran di salah satu perguruan tinggi favorit di kotanya. Salah satu persiapan yang dilakukannya adalah mengikuti program tryout online yang dilakukan oleh KPM. Pada kegiatan tersebut setiap paket tryout berisi 15 soal dengan nilai 10 untuk setiap jawaban benar dan -3 untuk jawaban salah dan 0 untuk soal yang tidak dijawab. Pada paket pertama Nala menjawab salah 2 soal dan tidak menjawab 2 soal. Sedangkan untuk paket kedua, dia mengerjakan semuanya dan menjawab benar 13 soal. Paket ketiga dia tidak menjawab 2 soal dan menjawab benar 12 soal. Berapakah nilai rata – rata Nala pada tryout tersebut?

5.      Terdapat 6 orang yang akan duduk di tiga baris kursi. Baris pertama terdiri dari 3 kursi, baris selanjutnya terdiri dari satu kurangnya dari banyak kursi di baris sebelumnya. Ada berapa banyak cara berbeda 6 orang tersebut duduk ?

6.      Pada system persamaan berikut,:

$pa + 2b - q - 1 = 0$

$a + b - 3 = 0$

dan

$2a + b - p^2 - 2 = 0$

$a + 3b - 3 = 0$

mempunyai solusi yang sama. Tentukan banyaknya pasangan bilangan $(p, q)$.

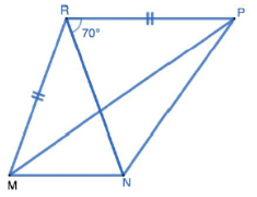
7.      Pada gambar berikut ini, diketahui sudut $RMN=70^o$, sudut $MRP=110^o$, sudut $NRP=70^o$, dan MR = RP. Berapa derajat besar sudut $MPN$? (Tulis jawaban angka saja tanpa derajat)

8.      Sistem mata uang Negara Pelangi sangat aneh: 1 koin merahnya sama dengan 5 dollar, 1 koin putih sama dengan 5 koin merah, 1 koin kuningnya sama dengan 5 koin putih, 1 koin hijaunya sama dengan 5 koin kuning. Satu koin biru sama dengan 5 koin hijau. Satu orang menukar semua mata uang Negara Pelangi dengan 2022 dollar, tetapi jumlah total koin yang diperlukan adalah yang paling sedikit, berapa banyak koin yang dia peroleh.

9.      Misalkan $S={1, 2, 3, ..., 9}$ dan A adalah himpunan bagian dari S yang terdiri dari 4 bilangan dan hasil perkalian semua anggota A adalah bilangan genap. Berapa banyak himpunan A yang dapat dibuat?

10. Jumlah dua akar dari persamaan kuadrat $x^2 - 4ax -b^2 + 4a^2=0$ adalah 12. Jika kedua akar tersebut merupakan bilangan bulat positif, berapa selisih terbesar kedua akar tersebut.

11. Diketahui:

$\frac{1}{3}+\frac{2}{21}+\frac{3}{91}+\frac{4}{273}+...+\frac{10}{10.101}=\frac{a}{b}$

Tentukan nilai dari:

$\frac{b-1}{a}$

12. Nala memiliki suatu bilangan KPMS yang terdiri dari 4 – angka berbeda. Jika hasil kali semua angka – angkanya sama dengan 360, maka berapa banyak bilangan berbeda yang dapat dibuat Nala?

13. Pada gambar berikut, diketahui PQRS dan WXYZ adalah persegi. Luas daerah yang diarsir sama dengan 200 cm². Titik J, K, L, dan M berada pada sisi – sisi PQRS, sehingga JQ = KR = LS = MP = $\frac{1}{4}$PQ. Ruas garis JZ, KW, LX, dan MY sejajar dengan diagonal persegi sehingga W di JZ, Z di KW, Y di LX, dan Z di MY. Berapakah cm² luas segitiga KMS?

14. Seekor semut berada di titik sudut sebuah limas segitiga. Setiap 1 perpindahan, semut tersebut dapat melakukan perjalanan dari satu titik sudut sepanjang rusuk limas ke titik sudut lain yang berdekatan. Diketahui peluang semua tersebut kembali ke posisi semula setelah 4 perpindahan adalah $\frac{a}{b}$. Berapa nilai paling kecil dari a + b ?

15. Nala adalah seorang anak yang senang berbagi kepada teman – temannya. Suatu hari Nala mendapat beberapa kantong permen dengan berbagai jenis ukuran dari pamannya. Permen tersebut akan dibagikan kepada teman – temannya. Diketahui sekantong kecil permen berisi 6 permen, sekantong permen ukuran sedang berisi 9 permen, dan sekantong besar permen berisi 20 permen. Jika Nala hanya bisa memberi permen dalam kantong saja, berapa jumlah permen terbanyak yang tidak dapat diberikan kepada temannya secara tepat?

16. Pada segitiga ABC, diketahui panjang AB = 7, BC = 8, AC = 9. Titik D pada BC sehingga AD adalah garis tinggi. Titik E pada AC sehingga E adalah titik tengah AC. Titik F merupakan perpotongan ruas AD dan BE. Jika luas segitiga AEF = $\frac{a}{b}\sqrt c$, dengan $fpb(a, b)=1$ dan c bilangan prima, maka nilai dari a + b + c = ...

17. Raya membagikan buku ke tiga panti asuhan di sekitar rumahnya. Ia akan membagikan sepuluh buku matematika yang identik dan lima buku dongeng yang identik. Berapa banyak cara ia membagikan buku jika setiap panti asuhan setidaknya mendapat satu buku matematika dan satu buku dongeng serta banyaknya buku matematika di setiap panti asuhan lebih banyak dari buku dongeng?

18. Sebuah suku banyak $P_0, P_1, P_2, P_3, ..., P_n$ didefenisikan sebagai berikut:

$P_0(x)=x^2-x-2022$

$P_n(x)=P_{n-1}(x-n)$ untuk n bilangan asli

Tentukan koefisien x pada $P_6(x)$.

Untuk soal dalam bentuk Word, silahkan download di link berikut:

DOWNLOAD SOAL

Untuk Solusinya dalam bentuk Video, saksikan Video Berikut:

VIDEO PEMBAHASAN FULL

Share this post